京都池内式 曲消し率
曲消し率 1 (シミズ)
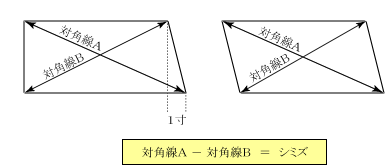
畳の寸法で対角線の差を、シミズといいます。このシミズの発生原因は、向かい合う辺の長さの違いによるものと、向かい合う辺の長さは同じでも、元々対角線の差によるもの(地シミズ)があります。後者の例をあげれば、菱形になるものがそれにあたります。
前者の場合、長さが1寸違えばどれ位シミズが掛かるかを計算します。
この計算をするのに、「三平方の定理」を利用します
曲消し率2 (三平方の定理)
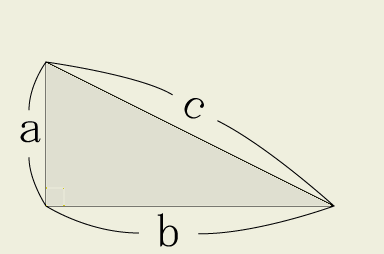
次のような直角三角形の三辺の長さについては
a2+b2=c2が成り立ちます(これを三平方の定理と言います)
曲消し率3(長方形・1畳)
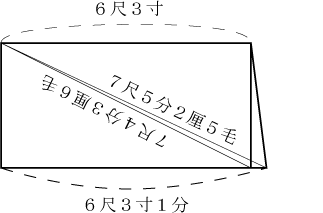
【1】 丈 6尺3寸 幅 3尺1寸5分の長方形(たたみ)の対角線は
即ち対角線の長さは、7尺4分6厘3毛です。
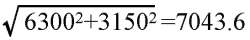
【2】 丈 6尺3寸1分 幅 3尺1寸5分の長方形(たたみ)の対角線は
即ち対角線の長さは、7尺5分2厘5毛です。
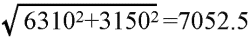
よって、丈の長さが10(1分)違えば、対角線に9厘の差が発生します。 言い換えれば、1寸長さが違うと、9分シミズが掛かることになります。 同じく幅を1寸変えたときには、上記の計算で、4分5厘になります。
だから 1畳の畳で1分長さが違うと、丈で0.9分、幅で0.45分シミズが掛かる この 0.9や0.45を曲消し率といいます。
曲消し率 4 (矩形・6畳)
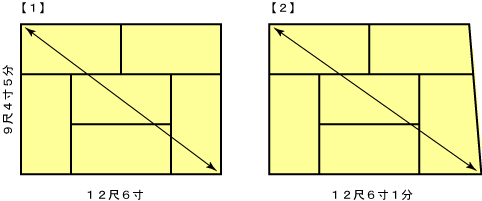
【1】の対角線は![]()
【2】の対角線は![]()
よって、6畳の場合、2間丈で長さが違うと、8厘のシミズが掛かる。
曲消し率 5 (矩形・6畳2)
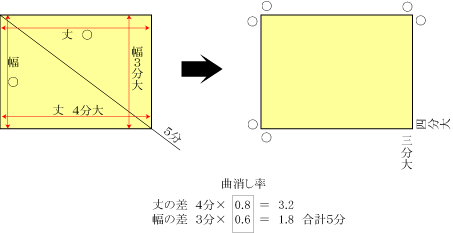
寸法の差を、丈・幅ともそれぞれの乗率で計算した数値の合計が、
シミズの数値と一致すれば割付の方法次第で、出会い框が曲無しになります。